RSA Cryptography

Why Public Key Cryptography?

Cryptography can be studied from many different points of view.

Many points of view in Cryptography (1/2)

Based on the services offered

• Confidentiality
• Integrity
• Authentication
• Protection against replay attacks
• …

Many points of view in Cryptography (2/2)

Based on the ways keys are managed

• Symmetric key cryptography
• Asymmetric key cryptography

All algorithms based on symmetric key cryptography assume to be working with a symmetric key that is shared across all the entities that need to communicate.

Encryption/Decryption in symmetric cryptography

\[\begin{split} \text{(plaintext) } p &\longrightarrow \text{ENCRYPT}(p, k) &= c \text{ (ciphertext)} \\ \\ \text{(ciphertext) } c &\longrightarrow \text{DECRYPT}(c, k) &= p \text{ (plaintext)} \\ \end{split}\]

The problem is…

This is essentially impossible to solve if you consider a situation in which you want to communicate securely with someone you have never met and can't possibly meet in other ways.

Q: Is it possible to communicate securely if you have not been able to share a symmetric key beforehand?

A: Yes, it is!

Thanks to Asymmetric Cryptography!

Introduced by Whitfield Diffie and Martin Hellman in 1976, asymmetric cryptography has been a huge leap forward for cryptography.

https://ee.stanford.edu/~hellman/publications/24.pdf

The paper introduced the idea of asymmetric cryptography, also known as public-key cryptography as well as the notion of one-way trapdoor functions.

The paper also discussed a pratical technique that allowed to

The technique introduced is now known as the

Diffie-Hellman Key Exchange (DH)

and it is used in many practical context, including SSL/TLS.

Historical Note

Even though the first public paper of such ideas was published in \(1976\) by Whitfield Diffie and Martin Hellman, the same ideas were independently discovered at GCHQ some years earlier around \(1973\).

https://cryptome.org/ukpk-alt.htm

Asymmetric cryptography is based on the generation of two keys \(k_1, k_2\) such that:

• All that is encrypted by one of the key can only be decrypted by the other.
• Out of the two keys, only one can be used to derive the other efficiently.

Out of the two keys, \(k_1, k_2\), we call

• private key, the key that allows us to generate the other key efficiently.
• public key, the remaining key.

For example, given \(k_1, k_2\), if we can use \(k_1\) to generate \(k_2\), then we call \(k_1\) the private key, and \(k_2\) the public key.

Reraphrasing…

In asymmetric cryptography we have two keys, a private key, and a public key. From the private key we can efficiently compute the public key, but from the public key we cannot efficiently compute the private key.

RSA is one of the first examples of a complete public-key cryptosystem that can be used for:

• confidentiality
• integrity
• authentication

Hands-On Introduction to RSA

Before describing the formal theory let us see some pratical examples.

Suppose, for your own protection, that you want to encrypt the following message

\[\text{The tutor of CNS sucks at teaching}\]

In RSA, everything is a number.

More specifically, everything is a number in some

modular group \(\mathbb{Z}_n\)

Modular Arithmetic

In traditional arithmetic we consider sets made up of infinite numbers, such as

• the set of natural numbers

  \[\mathbb{N} = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, \ldots\}\]

• the set of integers

  \[\mathbb{Z} = \{0, 1, -1, 2, -2, 3, -3, \ldots\}\]

The problem is that

computers have only a finite memory

To fix this problem, we introduce the modular group \(\mathbb{Z}_n\), which is a well known and studied algebraic structure that has only has a finite number of possible values.

Anatomy of \(\mathbb{Z}_n\):

• It contains \(n\) different values

  \[\mathbb{Z}_n = \{0\;\;, 1\;\;,\;\; \ldots, \;\; n-1\}\]

• Traditional operations replaced with modular operations

  \[\begin{split} 3 + 7 \mod 5 &= 10 \mod 5 \\ &= 0 \mod 5 \end{split}\]

Modular operations works as follow:

• First we perform the operation as usual
• Then we take the remainder when dividing the previous number with \(n\)

Some examples

\[\begin{split} 3 + 10 \mod 3 &= 13 \mod 3 = 1 \mod 3\\ 5 + 13 \mod 4 &= 18 \mod 4 = 2 \mod 4\\ \\ 3 * 10 \mod 6 &= 30 \mod 6 = 0 \mod 6\\ 2 * 17 \mod 7 &= 34 \mod 7 = 6 \mod 7\\ \end{split}\]

When working with modular arithmetic \(\mathbb{Z}_n\), the number of the modulus \(n\) assumes a very critical role.

In particular, it matters whether \(n\) is a prime or not.

Modular arithmetic can be visualized as clock arithmetic.

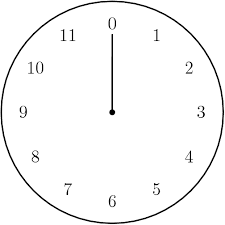
\[\mathbb{Z}_{12} = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11\}\]

Remember our objective was to encrypt the dangerous message

\[\text{The tutor of CNS sucks at teaching}\]

How do we go from the message text to a number in some \(\mathbb{Z}_n\)?

RSA keys

Given that RSA is a public-key cryptography system, we have two keys:

• A private key, an integer \(d\)
• A public key, composed of two integers \((e, N)\)

Before encrypting our message we have to obtain the public key of the future receiver of the message.

RSA Keys

\[d \;\;,\;\; (e, N)\]

The number \(N\) represents the modulus we're working with.

\[\mathbb{Z}_N = \{0, 1, 2, 3, \ldots, N-1\}\]

In our case, suppose our friend has the following public key

E = 65537
N = 12357441190498766132449640928501623256469111823853059262686903
    98208897117161516169208029001141055036840287816737238820534004
    76571357110578897839565426525836523516069897401769498818606567
    64127057886348459910372317288627711800953192434659136679611816
    8388195224114860554824660954136393556092086822258328661660329

What's up with the BIGGGG N?

The value \(N\) is actually obtained by multiplying two prime numbers \(P\) and \(Q\)

\[N = P \cdot Q\]

For a secure system, \(P\) and \(Q\) must be very bigggg \((> 1024 \text{ bits})\).

In our particular case

P = 981569731816206792118534210498736452673485598320277985759240
    562937996692473211773715586961068632843455578733065632271110
    2820785964943055892282853176094089

Q = 125894684707052732634619731920748998199627974572082321922141
    493623930038453609550986925916569721523263558109451542514916
    67000321296926470121976969660208161

NOTE: not showing full numbers because of space…

\[\begin{split} P \cdot Q &= (9815 \cdots 4089) \cdot (1258 \cdots 8161) \\ &= (1235 \cdots 0329) \\ &= N \\ \end{split}\]

Code to generate RSA keys

from Crypto.PublicKey import RSA

def generate_key(bits):
    KEY = RSA.generate(BIT_SIZE)
    return KEY

(code/example_1_rsa_hands_on.py)

Code to print information about RSA key

def dump_key(rsa_key):
    print("Private parameters")
    print(f"D={rsa_key.d}")
    print(f"P={rsa_key.p}")
    print(f"Q={rsa_key.q}")
    print("Public parameters")
    print(f"N={rsa_key.n}")
    print(f"E={rsa_key.e}")
    print("==========================")

(code/example_1_rsa_hands_on.py)

Real example of RSA parameters (1024 bits)

Private parameters

D = 7761465630161671436394072733256756752588763834923044263551118988704659594604713263
    5038976089031658382193794736479535148436716921258023165599315212961676134453005072
    5986827108953721558434941732038437591573053924491754510126364959317607757682447820
    942988657535279905936373267774215782242998025429793627422113

P = 9815697318162067921185342104987364526734855983202779857592405629379966924732117737
    155869610686328434555787330656322711102820785964943055892282853176094089

Q = 1258946847070527326346197319207489981996279745720823219221414936239300384536095509
    8692591656972152326355810945154251491667000321296926470121976969660208161

Public parameters

N = 1258946847070527326346197319207489981996279745720823219221235744119049876613244964
    0928501623256469111823853059262686903982088971171615161692080290011410550368402878
    1673723882053400476571357110578897839565426525836523516069897401769498818606567641
    2705788634845991037231728862771180095319243465913667961181683881952241148605548246
    60954136393556092086822258328661660329

E = 65537

To go from the message \(m\) to a number in \(\mathbb{Z}_n\) without using any padding schemes we can directly use the underlying bytes of the message.

For example

\[\begin{split} \text{The} &\longrightarrow \text{T h e} &\text{ ascii}\\ &\longrightarrow \texttt{54 68 65} &\text{ (base16)}\\ &\longrightarrow \texttt{01010100 01101000 01100101} &\text{ (base2)}\\ &\longrightarrow \texttt{5531749} &\text{ (base10)}\\ \end{split}\]

After we have obtain the final number, we have to reduce it modulo \(N\)

\[\text{The} \longrightarrow \texttt{5531749} \longrightarrow \texttt{5531749} \mod N\]

In our example

\[\text{The tutor of CNS sucks at teaching}\]

becomes

Encryption/Decryption in RSA

In RSA, encryption and decryption are done through modular exponentiation.

\[a^b \mod N\]

Some examples of modular exponentiation

• \(2^{10} \mod 5 = 1024 \mod 5 = 4\)
• \(5^{3} \mod 7 = 125 \mod 7 = 6\)

In particular, when we want to encrypt a message \(m\) using the public key \((e, N)\), we compute the following

\[m^e \mod N\]

In our case example this value is

\[(250208 \cdots 36327)^{65537} \mod (1235 \cdots 0329)\]

Code to encrypt using RSA

def encryption_example(key, plaintext):
    print(f"About to encrypt a new message")
    print(f"Plaintext:\n{plaintext}")
    ciphertext = pow(plaintext, key.e, key.n)
    print(f"Ciphertext:\n{ciphertext}")
    print("==========================")
    return ciphertext

(code/example_1_rsa_hands_on.py)

Once we have the encrypted message, which is just a number, we can transmit it over the network to the receiver.

To get back the original message, the receiver will start from the ciphertext message \(c\) and use its own private key \(d\) to compute

\[c^d \mod N\]

Code to decrypt using RSA

def decryption_example(key, ciphertext):
    print(f"About to decrypt a new message")
    print(f"Ciphertext:\n{ciphertext}")
    plaintext = pow(ciphertext, key.d, key.n)
    print(f"Plaintext:\n{plaintext}")    
    print("==========================")
    return plaintext

(code/example_1_rsa_hands_on.py)

The mathematics of RSA guarantess that by doing this computation we get back the original message \(m\).

\[c^d \mod N = m\]

Putting everything toget we get

def encryption_decryption_test():
    key = generate_key(BIT_SIZE)
    dump_key(key)
    m = b"The tutor of CNS sucks at teaching"
    p = bytes_to_long(m)
    c = encryption_example(key, p)
    p2 = decryption_example(key, c)
    assert p == p2, "Oops, we broke math"

(code/example_1_rsa_hands_on.py)

Let us now formalize what we saw…

RSA in Theory

RSA is a public-key based cryptographic system that can be used for

• confidentiality
• integrity
• authentication

It was discovered in 1977 by

\[\begin{split} \text{R} &\longrightarrow \text{Rivest} \\ \text{S} &\longrightarrow \text{Shamir} \\ \text{A} &\longrightarrow \text{Adleman} \\ \end{split}\]

RSA makes use of mathematical theorems taken from number theory for

• correctness
• security

When working with RSA, the following holds:

• Messages are seen as numbers.
• All work is done in a modular arithmetic.
• Encryption and decryption are implemented through modular exponentiation.

Process of generating a public/private key in RSA

Here with \(\Phi(N)\) we mean Euler's totient function, which simply counts the number of integers in \(\{1, 2, \ldots, N-1\}\) which are relatively prime to \(N\).

\[\begin{split} \Phi(3) &= 2 \\ \Phi(10) &= 4 \\ \Phi(7) &= 6 \\ \end{split}\]

If \(N = p \cdot q\), where \(p\) and \(q\) are primes, then

\[\Phi(N) = (p - 1) \cdot (q - 1)\]

To encrypt a message \(m \in [0, N)\) we use modular exponentiation

\[c = m^e \mod N\]

NOTE: Everyone can encrypt messages, as \((e, N)\) is the public key.

To decrypt an encrypted message \(c \in [0, N)\) we proceed once again with modular exponentiation

\[m = c^d \mod N\]

NOTE: Only the owner of the private key \(d\) can decrypt messages.

Let us now motivate two important aspects of RSA, which are:

• correctness
• security

RSA correctness

By correctness we mean the fact that we can use RSA to encrypt and decrypt properly. That is, we want to make sure that encryption is a revertable process.

In particular, remember the encryption procedure

\[c = m^e \mod N\]

When we decrypt we are computing a power of \(m\)

\[\begin{split} c^d \mod N &= (m^e)^d \mod N \\ &= m^{e \cdot d} \mod N \end{split}\]

Formally to have correctness we want

\[m^{e \cdot d} \mod N = m \mod N\]

The correctness of RSA relies on the Euler's Theorem

Given an integer \(a\) such that \(gcd(a, N) = 1\), then

\[a^{\Phi(N)} \equiv 1 \mod N\]

We know that the parameters were choosen such that

\[d \equiv e^{-1} \mod \Phi(N)\]

which means that

\[e \cdot d \equiv 1 \mod \Phi(N)\]

That is, there exists \(k \in \mathbb{Z}\) such that

\[e \cdot d = k \cdot \Phi(N) + 1\]

Putting it all together

Security of RSA

The security of RSA is based on the computational intractability of the factorization problem.

Remember, the public key of RSA is \((N, e)\).

Can an attacker use the public key to obtain the private key?

By knowing only \((N, e)\), we're not able to compute the private key \(d\), because \(d\) was computed as the solution of the following congruence

\[d \equiv e^{-1} \mod \Phi(N)\]

To solve

\[d \equiv e^{-1} \mod \Phi(N)\]

we need to know the value of \(\Phi(N)\).

And to know the value of \(\Phi(N)\) we need to know the prime factors of \(N\), as

\[\Phi(N) = (P - 1) \cdot (Q - 1)\]

This requires being able to factorize \(N\) into its prime factors.

This also means that the security of our system completely depends on the characteristics of the choosen primes \(p\) and \(q\).

To have a secure RSA the primes must be:

1. Very bigggggggg
2. Distant from eachothers

RSA Signature

RSA can also be used to sign messages.

RSA can also be used to sign messages (1/8)

Let \(d\) be our private key, and \((e, N)\) be our public key.

From a message \(m\), we want to compute a signature such that other entities can verify if our signature is valid.

RSA can also be used to sign messages (2/8)

To compute the signature of the message \(m\) we encrypt it using our private key as follows

\[s = m^d \mod N\]

RSA can also be used to sign messages (3/8)

This allows any other entity to check if the signature \(s\) is valid for message \(m\) by using our private key \((e, N)\) as follows

\[\begin{split} s^e \mod N = m \;\;? \begin{cases} \text{yes } &\implies \text{ valid signature } \\ \text{no } &\implies \text{ invalid signature } \\ \end{cases} \end{split}\]

RSA can also be used to sign messages (4/8)

Instead of signing the entire message \(m\), it is preferable to first use an hash function, compute \(H(m)\), and then sign the resulting value.

RSA can also be used to sign messages (5/8)

\[m \longrightarrow H(m) \longrightarrow \underbrace{H(m)^d \mod N}_{\text{ signature for } m }\]

RSA can also be used to sign messages (6/8)

def compute_signature(msg, key):
    hash_value = sha256(msg.encode('utf-8'))
    bytes_value = codecs.decode(hash_value.hexdigest(), 'hex_codec')
    hash_number = bytes_to_long(bytes_value) % key.n
    signature_value = pow(hash_number, key.d, key.n)
    return (msg, signature_value)

(code/example_2_rsa_signature.py)

RSA can also be used to sign messages (7/8)

def verify_signature(signature, key):
    (msg, sig_value) = signature
    
    hash_value = sha256(msg.encode('utf-8'))
    bytes_value = codecs.decode(hash_value.hexdigest(), 'hex_codec')
    hash_number = bytes_to_long(bytes_value) % key.n    

    signature_check = pow(sig_value, key.e, key.n)

    if hash_number == signature_check:
        print("OK: Signature correctly verified!")
    else:
        print("NOPE: Signature failed!")

(code/example_2_rsa_signature.py)

RSA can also be used to sign messages (8/8)

def main():
    global BIT_SIZE
    key = RSA.generate(BIT_SIZE)
    msg = "Hello World!"
    signature = compute_signature(msg, key)
    verify_signature(signature, key)    

(code/example_2_rsa_signature.py)

Final Overview

Final recap of RSA Theory (1/4)

• RSA makes use of modular arithmetic
• RSA key requires two big and distant primes \(p, q\)
• Public parameters are \((e, N)\) such that
  • \(N=p \cdot q\)
  • \(gcd(e, \Phi(N))=1\)

• Private parameter \(d\) obtained by solving

  \[d \equiv e^{-1} \mod \Phi(N)\]

Final recap of RSA Theory (2/4)

• Encryption and decryption implemented through modular exponentiation.

• To encrypt

  \[c = m^e \mod N\]

• To decrypt

  \[m = c^d \mod N\]

Final recap of RSA Theory (3/4)

• Digital signature implemented by encrypting with private key.

  \[s = H(m)^d \mod N\]

• To verify a digital signature \((m, s)\) we use the public key

  \[s^e \mod N == H(m) \;\; ?\]

Final recap of RSA Theory (4/4)

• Security guaranteed as long as we cannot factorized \(N\) into its prime factors \(p\) and \(q\)

RSA in Practice

Many things can go wrong when implementing RSA in the real and scary world.

In the real world RSA is used a long side a padding scheme such as:

• PKCS#1v1.5 (dangerous)
• OAEP

The PKCS#1v1.5 padding scheme has been found to be vulnerable time and time again to a certain padding oracle attack known as the

Bleichenbacher oracle attack

(maybe we will see it in a future lecture)

A small and incomplete list of possible RSA implementation failures

Fermat Attack by Hanno Böck (Marh 2022)

https://fermatattack.secvuln.info/

To practice with some RSA related CTF I highly suggest the cryptohack website

https://cryptohack.org/

CTF 01 – Factoring

RSA – PRIMES PART 1 – Factoring

https://cryptohack.org/challenges/rsa/

In the challenge we are asked to factorize the following \(150\) bit number into its two-constituent primes.

To solve the challenge we can use sage, and open-source mathematical system which can be used to solve many mathematical problems.

Installing sage

sudo apt install sagemath # on ubuntu
yay -S sagemath           # on archlinux

Using sage

[leo@ragnar ~]$ sage
┌────────────────────────────────────────────────────────────────────┐
│ SageMath version 9.7, Release Date: 2022-09-19                     │
│ Using Python 3.10.8. Type "help()" for help.                       │
└────────────────────────────────────────────────────────────────────┘
sage: F = factor(510143758735509025530880200653196460532653147)
sage: F
19704762736204164635843 * 25889363174021185185929

In a few seconds we can break a \(150\) bit composite number into its factor components

CTF 02 – Monoprime

RSA – PRIMES PART 1 – Monoprime

https://cryptohack.org/challenges/rsa/

If we use only \(1\) prime \(N=p\), then we can easily compute \(\Phi(N)\) as

\[\Phi(N) = \Phi(p) = p-1\]

and therefore easily compute

\[d \equiv e^{-1} \mod \Phi(p)\]

Using the challenge parameters and sage we obtain

sage: N = 17173137121806544412548253630224591541560331838028039238529183647229975274793460724647750850782728407576
....: 391026499532601025126849363050198981085541841664335263110243431790002869799322486862993565727306247254467569
....: 3365930943308086634291936846505861203914449338007760990051788980485462592823446469606824421932591
sage: R = IntegerModRing(N-1)
sage: R(65537)^(-1)
4907958226519928847018154485162680616650518261840871186316914257787470236612623699172259539422929079358313684275084999575821686811571024412404171669352777812198526931007320349593989810014859842319185284817373049936286199502815909578235160497207349053691252423646739007995495070712291321823019631255354109583

In particular we get

D = 490795822651992884701815448516268061665051826184087118631691
    425778747023661262369917225953942292907935831368427508499957
    582168681157102441240417166935277781219852693100732034959398
    981001485984231918528481737304993628619950281590957823516049
    720734905369125242364673900799549507071229132182301963125535
    4109583

With the private key we're able to decrypt our text

[leo@ragnar 3_monoprime]$ python
Python 3.10.8 (main, Oct 13 2022, 21:13:48) [GCC 12.2.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> from Crypto.Util.number import bytes_to_long, long_to_bytes
>>> D = 490795822651992884701815448516268061665051826184087118631691425778747023
86811571024412404171669352777812198526931007320349593989810014859842319185284817
3646739007995495070712291321823019631255354109583
>>> N = 171731371218065444125482536302245915415603318380280392385291836472299752
84936305019898108554184166433526311024343179000286979932248686299356572730624725
007760990051788980485462592823446469606824421932591
>>> CT = 16136755034673060445145475618902893896494128034766209879877546601946337
21011578171525759600774739890458414593857709994072516290998135846956596662071379
6260758515864509435302781735938531030576289086798942  
>>> PT = pow(CT, D, N)
>>> long_to_bytes(PT)
b'crypto{0n3_pr1m3_41n7_pr1m3_l0l}'

The flag is

      crypto{0n3_pr1m3_41n7_pr1m3_l0l}