Breaking PRNGs for Fun and Profit

Introduction

Hello.

$ whoami

I'm Leonardo Tamiano, a PhD researcher here at Tor Vergata.

I work with professor Giuseppe Bianchi and I will be your teaching assistant for

Sicurezza delle Infrastrutture ICT (SII)

Teaching material such as slides, code, exercises and general material can be found at the following URL

For doubts and questions, I'm available after lectures.

Also, feel free to send me emails to the following email address

\[\text{leonardo.tamiano@cnit.it}\]

But, please, put the following in the subject line

\[\text{[SII]}\]

Today we will try to make sense of randomness

What is Randomness?

Many applications require the generation of random numbers for various purposes:

• Generation of cryptographic material
• Simulation and modelling of complex systems
• Sampling from large data sets

Cool, but…

what exactly is randomness?

What exactly is randomness?

For example, are these random numbers?

\[\begin{split} &1338 \; \rightarrow \; 890 \; \rightarrow \; 1632 \\ &\;\;\;\;\;\;\; \rightarrow 1144 \; \rightarrow \; 918 \; \rightarrow \; 2068 \\ &\;\;\;\;\;\;\; \rightarrow 878 \; \rightarrow \; 1002 \; \rightarrow \; 1386 \\ &\;\;\;\;\;\;\; \rightarrow \text{???} \; \rightarrow \; \text{???} \; \rightarrow \; \text{???} \\ \end{split}\]

Are you able to continue the sequence?

Are you able to correctly predict the next number?

Those numbers were generated starting from the names of Metro B subway stations in Rome, from "Laurentina" to "Termini"

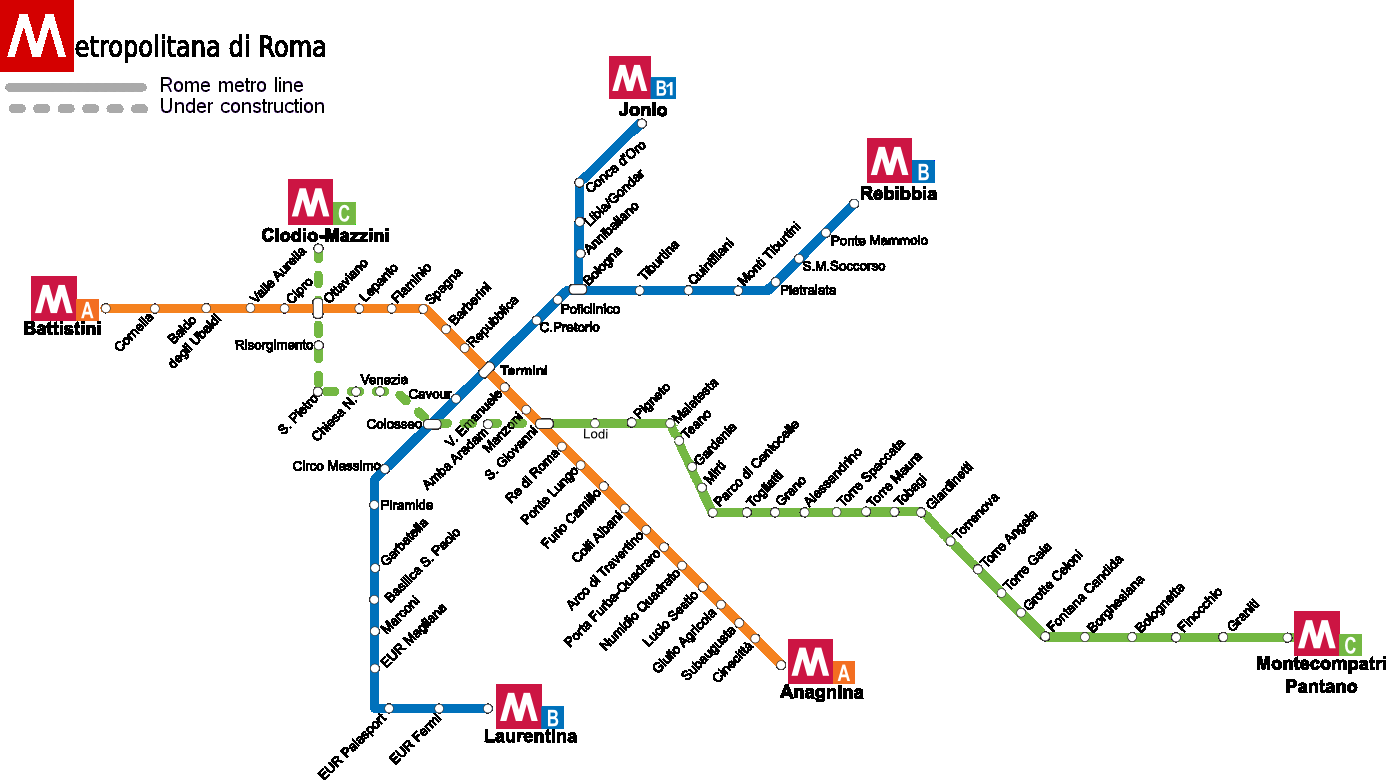
From station names to numbers (1/4)

1. From the metro station name to a sequence of numbers using the underlying ASCII encoding.
2. Combine these numbers with mathematical operations.

From station names to numbers (2/4)

Metro station names \(\longrightarrow\) numbers, using the underlying ASCII encoding

\[\begin{split} \text{T} &\longrightarrow 84 \;\;,\;\; \text{e} &\longrightarrow 101 \;\;,\;\; \text{r} &\longrightarrow 114 \\ \text{m} &\longrightarrow 109 \;\;,\;\; \text{i} &\longrightarrow 105 \;\;,\;\; \text{n} &\longrightarrow 110 \\ \text{i} &\longrightarrow 105 \\ \end{split}\]

From station names to numbers (3/4)

Then, we combine those numbers with basic mathematical operations.

\[\begin{split} 109 \mathbin{\oplus} 84 &= (\text{1101101})_2 \mathbin{\oplus} (\text{1010100})_2 \\ &= \text(0111001)_2 \\ &= 57 \end{split}\]

From station names to numbers (4/4)

For example,

\[\begin{split} \text{Hi} &\longrightarrow 72 \;\; 105 \\ &\longrightarrow ((((0 \mathbin{\oplus} 72) + 72) \mathbin{\oplus} 105) + 105) \\ &\longrightarrow (((72 + 72) \mathbin{\oplus} 105) + 105) \\ &\longrightarrow ((144 \mathbin{\oplus} 105) + 105) \\ &\longrightarrow (249 + 105) \\ &\longrightarrow 354 \\ \end{split}\]

This is the relevant code

#!/usr/bin/env python3
subway_B = ["laurentina", "EUR Fermi", "EUR Palasport", "EUR Magliana",
            "Marconi", "Basilica S. Paolo", "Garbatella", "Piramide",
             "Circo Massimo", "Colosseo", "Cavour", "Termini" ]

def station_to_number(station_name):
    result = 0
    for c in station_name:
        result = (result ^ ord(c)) + ord(c) #!
    return result

if __name__ == "__main__":
    for metro_station in subway_B:
        print(station_to_number(metro_station))

(code/subway2seq.py)

We are thus able to complete the sequence

\[\begin{split} &1338 \; \rightarrow \; 890 \; \rightarrow \; 1632 \\ &\; \rightarrow 1144 \; \rightarrow \; 918 \; \rightarrow \; 2068 \\ &\; \rightarrow 878 \; \rightarrow \; 1002 \; \rightarrow \; 1386 \\ &\; \rightarrow 1078 \; \rightarrow \; 824 \; \rightarrow \; 912 \\ \end{split}\]

Weird but completely deterministic pattern

Definitely not random!

Q: What is randomness? (1/5)

A1:

"Something is random if and only if it happens by chance"

Reaction: no sh!t, Sherlock.

What do you mean with "chance"?

Q: What is randomness? (2/5)

A2:

"scientists use chance, or randomness, to mean that when physical causes can result in any of several outcomes, we cannot predict what the outcome will be in any particular case." (Futuyma 2005: 225)

Reaction: blah, blah, blah…

Q: What is randomness? (3/5)

Hard to define precisely.

Q: What is randomness? (4/5)

Practical definition:

Randomness is something that is "hard" to predict.

Q: What is randomness? (5/5)

As a consequence,

And here comes the first term

\[\begin{split} \text{TRNG} &\longrightarrow \text{Truly} \\ &\longrightarrow \text{Random} \\ &\longrightarrow \text{Number} \\ &\longrightarrow \text{Generator} \\ \end{split}\]

TRNGs sample phenomena from the physical world to generate values that are "pratically" unpredictable.

Some examples:

• Nuclear decay
• Atmospheric noise
• …

And Pseudo-Randomness?

So far we have:

1. Random numbers are hard to generate
2. Yet, we still need to generate random numbers

How to bridge this gap?

How can computers generate randomness?

MAIN IDEA: use an approximation!

Consider the following sequence of numbers

\[292616681 \rightarrow 1638893262 \rightarrow 255706927 \rightarrow \ldots\]

Do you see any pattern?

\[292616681 \rightarrow 1638893262 \rightarrow 255706927 \rightarrow \ldots\]

While these numbers do look random, they are generated through a completely deterministic process using a PRNG

\[\text{PRNG} \longrightarrow \text{Pseudo Random Number Generator}\]

The previous numbers can be generated deterministically with the following C code

#include <stdlib.h>
#include <stdio.h>

int main(void) {
  srand(1337);
  int n = 10;

  for (int i = 0; i < n; i++) {
    printf("%d\n", rand());
  }

  return 0;
}

(code/rand_example.c)

\[292616681 \rightarrow 1638893262 \rightarrow 255706927 \rightarrow \ldots\]

[leo@ragnar code]$ gcc rand_example.c -o rand_example

[leo@ragnar code]$ ./rand_example 
292616681
1638893262
255706927
995816787
588263094
1540293802
343418821
903681492
898530248
1459533395

The sequence generated by a PRNG is completely determined by internal state of the PRNG and the initial seed value, which initializes the internal state

\[\text{seed} \longrightarrow \text{PRNG} \longrightarrow \text{output}_0, \text{output}_1, \ldots\]

C rand() with different seeds

\[\begin{split} 1337 &\longrightarrow &292616681, \;\; &1638893262, \;\; &255706927, \ldots \\ 5667 &\longrightarrow &1971409024, \;\; &815969455, \;\; &1253865160, \ldots \\ 42 &\longrightarrow &71876166, \;\; &708592740, \;\; &1483128881, \ldots \\ \end{split}\]

This is the idea behind PRNGs and, more in general, pseudo-randomness and pseudo-random sequences:

• having a sequence of numbers that looks random
• yet it is completely determined by
  • an underlying algorithm
  • the initial seed value

Some important terms in the context of PRNGs:

• state: total amount of memory that is used internally by the PRNG to generate the sequence of numbers.
• period: after how many numbers the PRNG resets to its initial "state".

Not all about looks, even for PRNGs.

Good PRNGs satisfy specific statistical properties.

Q: Do basic PRNGs also satisfy security related cryptographic properties?

Said in another way…

given an output of the PRNG, are we able to predict the next number?

\[x_n \longrightarrow \;\; ?\]

Q: Do basic PRNGs also satisfy security related cryptographic properties?

• Short answer: No.
• Long answer: No, and this is problematic…

We will see why using PRNGs in certain contexts could be dangerous.

Now, there are many PRNGs:

• Middle-square method (1946)
• Linear Congruential Generators (1958)
• Linear-feedback shift register (1965)
• …
• Mersenne Twister (1998)
• xorshift (2003)
• xoroshiro128+ (2018)
• squares RNG (2020)

To understand how PRNGs work we will analyze two specific implementations:

• rand(), implemented in C. (today)

  #include <stdlib.h>
  seed(1337);
  printf("%d\n", rand()); // 292616681
  

• getrandbits(), implemented in python. (next lecture)

  import random
  random = random.Random(1337)
  print(random.getrandbits(32))  # 2653228291
  

But first, let us consider a simple example.

A First PRNG: Middle Square Method

It works as follows:

• a \(n\) digit number is given in input as a seed
• to produce the next number:
  • square the seed
  • add leading zeros to reach a \(2n\) digit number
  • return the \(n\) middle digits
  • the returned number becomes the new seed

For example,

Some sequences with different seeds,

\[\begin{split} 675248 &\longrightarrow &959861, \;\; &333139, \;\; &981593, \ldots \\ 1337 &\longrightarrow &7875, \;\; &156, \;\; &243, \ldots \\ 42&\longrightarrow &76, \;\; &77, \;\; &92, \ldots \\ \end{split}\]

Is it statistically useful?

Not really, as it usually has a short period.

Also, the value of \(n\) must be even in order for the method to work. (can you see why?)

state: total amount of memory that is used internally by the PRNG to generate the sequence of numbers.

Q: How big is the state for the Middle Square Method?

A: The memory necessary to store the \(n\) digit number, which is at most…

\[\log_2(10^n - 1)\]

Is it cryptographically secure?

no (trivially).

Exercise (optional): implement the Middle Square Method PRNG using a programming language you desire.

Prefered options are Python or C.

A Second PRNG: Linear Congruential Generator

Consider the code of before

#include <stdlib.h>
#include <stdio.h>

int main(void) {
  srand(1337);
  int n = 10;

  for (int i = 0; i < n; i++) {
    printf("%d\n", rand());
  }

  return 0;
}

(code/rand_example.c)

If we execute it, we get

[leo@ragnar code]$ gcc rand_example.c -o rand_example

[leo@ragnar code]$ ./rand_example 
292616681
1638893262
255706927
995816787
588263094
1540293802
343418821
903681492
898530248
1459533395

How are these numbers generated?

\[\begin{split} &292616681, \;\; &1638893262, \;\; &255706927 \\ &995816787, \;\; &588263094, \;\; &1540293802 \\ &343418821, \;\; &903681492, \;\; &898530248 \\ &1459533395, \;\; &\ldots \end{split}\]

The libc implementation of rand() has two distinct behaviors, depending on the value of an internal variable

buf->rand_type

• If it is equal to \(0\), we have a simple

  Linear Congruential Generator

• Otherwise, we have a more complex

  Additive Feedback Generator

By default rand() has the more complex behavior of an Additive Feedback Generator type of PRNG

srand(1337)
rand()

The LCG behavior has to be manually activated

#include <stdio.h>
#include <stdlib.h>

int main(void) {
  // initialize LCG
  char state1[8];             // !
  initstate(1337, state1, 0); // !
  setstate(state1);           // !
  
  // use the PRNG
  srand(1337);
  int n = 10;
  for (int i = 0; i < n; i++) {
    printf("%d\n", rand());
  }
  return 0;
}

(code/rand_lcg.c)

Q: How did you figure this out?

A: some research, using:

• search engines
• reading source code
• debugging with gdb

(for those interested, at the end of the lecture I will do an interactive debugging session).

Let us focus on the first, simpler case.

Linear Congruential Generator

A Linear Congruential Generator is defined by the following set of equations

\[\begin{cases} x_0 &= \text{seed} \\ x_n &= (x_{n-1} \cdot a + b) \mod c \\ \end{cases}\]

where

• \(a, b, c\) are typically fixed
• \(\text{seed}\) changes on every restart

The state is initialized with the given \(\text{seed}\), and it is then updated for generating each subsequent number.

\[\text{seed} = x_0 \longrightarrow x_1 \longrightarrow x_2 \longrightarrow x_3 \longrightarrow \ldots \longrightarrow x_n\]

Let's look at the LCG implemented in the libc…

LCG in rand()'s glibc

Initialization in __srandom_r()

int __srandom_r (unsigned int seed, struct random_data *buf) {
  int type;
  int32_t *state;
  // ...
  state = buf->state;
  // ...
  state[0] = seed;
  if (type == TYPE_0)
    goto done;
  // ...
}

(glibc/stdlib/random_r.c:161)

State update in __random_r()

int __random_r (struct random_data *buf, int32_t *result) {
  // ...
  if (buf->rand_type == TYPE_0) {
    int32_t val = ((state[0] * 1103515245U) + 12345U) & 0x7fffffff;
    state[0] = val;
    *result = val;
  }
  // ...
}

(glibc/stdlib/random_r.c:353)

The main equation of the glibc LCG is

where

\[\texttt{0x7fffffff} = 2147483647\]

\[= \underbrace{01111111111111111111111111111111}_{32 \text{ bit}}\]

Note that

\[x \;\;\; \& \;\;\; 2147483647\]

is equivalent to

\[x \;\;\; mod \;\;\; 2147483648\]

(see code/rand_equivalence.c)

Remember the concepts of period and state…

• The LCG state in C rand() is made up of a single 32 bit integer

• Thus it has a period of

  \[2^{31} - 1 = 2147483647\]

  (see code/rand_lcg_period.c)

NOTE: why only \(2^{31} - 1\) and not \(2^{32} - 1\)? Because the last bit is thrown away (ask the devs).

How to break LCG

Now that we know how a LCG works, we can begin to understand how to "break" it.

Remember that by "breaking a PRNG" we simply mean

being able to predict what's the next number in the sequence given some outputs obtained from the PRNG

\[x_1, x_2, \ldots, x_n \overset{?}{\longrightarrow} x_{n+1}\]

Remember the main equation of the LCG

\[x_n = (x_{n-1} \cdot a + b) \mod c\]

and consider the following attack scenarios:

1. We know all the parameters \(a, b\) and \(c\)
2. We know some of the parameters \(a, b\) and \(c\)
3. We don't know any of the parameters \(a, b\) and \(c\)

We'll cover how to deal with scenarios \(1\) and \(3\).

Scenario \(1\): We know all the parameters

Scenario \(1\): We know all the parameters \(a, b\) and \(c\)

This scenario is easy.

Why?

Scenario \(1\): We know all the parameters \(a, b\) and \(c\)

Let \(x_1, x_2, \ldots, x_n\) be a sequence of observed outputs from the PRNG. Then the next output is obtained by simply using the main LCG equation

\[x_{n+1} = (x_{n} \cdot a + b) \mod c\]

For example, assuming

\[a=1103515245 \;\;,\;\; b=12345 \;\;,\;\; c=2147483648\]

if we get an output \(x_n = 1337\) the next output will be

Scenario \(2\): We don't know any of the parameters

Scenario \(2\): We don't know the parameters \(a, b\) and \(c\)

This scenario is a bit more involved.

The attack we'll discuss is based on a cool property of number theory.

There are also other roads to attack LCGs, following the research published by George Marsaglia in \(1968\)

Article

We can sketch the general idea behind the attack:

• We first observe an output sequence \(x_0, x_1, \ldots, x_n\).
• Then we compute the modulus \(c\)
• Then we compute the multiplier \(a\)
• Then we compute the increment \(b\)

Step 1/3: Computing the modulus \(c\)

Computing \(c\) (1/11)

Let \(x_0, x_1, \ldots, x_n\) be the observed sequence of outputs. We define

\[\begin{split} t_n &:= x_{n+1} - x_n \;\;\;&,\;\;\; n = 0, \ldots, n-1 \\ \\ u_n &:= | t_{n+2} \cdot t_n - t^2_{n+1} | \;\;\;&,\;\;\; n = 0, \ldots, n-3 \\ \end{split}\]

Computing \(c\) (2/11)

Then with high probability we have that

\[c = \text{gcd}(u_1, u_2, u_3, \ldots, u_{n-3})\]

where

\[\text{gcd} \longrightarrow \text{Greatest Common Divisor}\]

Computing \(c\) (3/11)

Code to compute the modulus \(c\)

def compute_modulus(outputs):
    ts = []
    for i in range(0, len(outputs) - 1):
        ts.append(outputs[i+1] - outputs[i])
        
    us = []
    for i in range(0, len(ts)-2):
        us.append(abs(ts[i+2]*ts[i] - ts[i+1]**2))

    modulus =  reduce(math.gcd, us) #!
    return modulus

(code/attack_lcg.py)

Computing \(c\) (4/11)

Q: Why does that even work?

Computing \(c\) (5/11)

Remember how we defined \(t_n\)

\[\begin{split} t_n &= x_{n+1} - x_n \\ &= (x_n \cdot a + b) - (x_{n-1} \cdot a + b) \mod c \\ &= x_n \cdot a - x_{n-1} \cdot a \mod c \\ &= (x_n - x_{n-1}) \cdot a \mod c \\ &= t_{n-1} \cdot a \mod c \\ \end{split}\]

Computing \(c\) (6/11)

Thus we get

\[t_{n+2} = t_n \cdot a^2 \mod c\]

Computing \(c\) (7/11)

This means that

\[\begin{split} t_{n+2} \cdot t_n - t^2_{n+1} &= (t_n \cdot a^2) \cdot t_n - (t_n \cdot a)^2 \mod c \\ &= (t_n \cdot a)^2 - (t_n \cdot a)^2 \mod c \\ &= 0 \mod c \\ \end{split}\]

Computing \(c\) (8/11)

Therefore \(\exists k \in \mathbb{Z}\) such that

\[u_n = |t_{n+2} \cdot t_n - t^2_{n+1}| = |k \cdot c|\]

Said in another way

\(u_n\) is a multiple of \(c\)!

Computing \(c\) (9/11)

Ok, with this we now know we can compute a bunch of multiples of \(c\) starting from a sequence of outputs

\[\begin{split} x_0, x_1, \ldots, x_n &\longrightarrow t_0, t_1, \ldots, t_{n-1} \\ &\longrightarrow \underbrace{u_0, u_1, \ldots, u_{n-3}}_{\text{multiples of $c$}} \\ \end{split}\]

Computing \(c\) (10/11)

And here comes the cool number theory fact:

The gcd of two random multiples of \(c\) will be \(c\) with probability

\[\frac{6}{\pi^2} \approx 0.61\]

Computing \(c\) (11/11)

By taking the gcd of many random multiples of \(c\), there is a very high probability that such gcd will be exactly \(c\).

\[c = \text{gcd}(u_1, u_2, u_3, \ldots, u_{n-3})\]

The more multiples we have, the higher the probability!

Step 2/3: Computing the multiplier \(a\)

Computing \(a\) (1/3)

Once we have the modulus \(c\), we can obtain the multiplier \(a\) by observing that

\[\begin{cases} x_1 &= (x_0 \cdot a + b) \mod c \\ x_2 &= (x_1 \cdot a + b) \mod c \\ \end{cases}\]

gives us

\[x_1 - x_2 = a \cdot (x_0 - x_1) \mod c \]

Computing \(a\) (2/3)

And from

\[x_1 - x_2 = a \cdot (x_0 - x_1) \mod c \]

we get

\[a = (x_1 - x_2) \cdot (x_0 - x_1)^{-1} \mod c\]

Computing \(a\) (3/3)

Code to compute the multiplier \(a\)

def compute_multiplier(outputs, modulus):
    term_1 = outputs[1] - outputs[2]
    term_2 = pow(outputs[0] - outputs[1], -1, modulus) #!
    a = (term_1 * term_2) % modulus
    return a

(code/attack_lcg.py)

Step 3/3: Computing the increment \(b\)

Computing \(b\) (1/2)

Finally, once we know \(c\) and \(a\), we can easily obtain \(b\)

\[\begin{split} x_1 &= (x_0 \cdot a + b) \mod c \\ &\implies \\ b &= (x_1 - x_0 \cdot a) \mod c \\ \end{split}\]

Computing \(b\) (1/2)

Code to compute the increment \(b\)

def compute_increment(outputs, modulus, a):
    b = (outputs[1] - outputs[0] * a) % modulus
    return b

(code/attack_lcg.py)

Putting it all together

def main():
    prng = LCG(seed=1337, a=1103515245, b=12345, c=2147483648)
    n = 10
    outputs = []
    for i in range(0, n):
        outputs.append(prng.next())
    # -----------------------------
    c = compute_modulus(outputs)
    a = compute_multiplier(outputs, c)
    b = compute_increment(outputs, c, a)
    print(f"c={c}")    
    print(f"a={a}")
    print(f"b={b}")

(code/attack_lcg.py)

We get

[leo@archlinux code]$ python3 attack_lcg.py 
c=2147483648
a=1103515245
b=12345

\[c=2147483648 \;\;, \;\; a=1103515245 \;\;, \;\; b=12345\]

LIVE DEMO

Wait a sec…

Let us implement a custom LCG in C with custom parameters

\[\begin{split} a &= 2147483629 \\ b &= 2147483587 \\ c &= 2147483647 \\ \end{split}\]

Custom LCG implementation (1/3)

uint32_t a = 2147483629;
uint32_t b = 2147483587;
uint32_t c = 2147483647;
uint32_t state;

uint32_t myrand(void) {
  uint32_t val = ((state * a) + b) % c;
  state = val;
  return val;
}

void mysrand(uint32_t seed) {
  state = seed;
}

(code/custom_lcg.c)

Custom LCG implementation (2/3)

int main(void) {
  mysrand(1337);
  int n = 10;
  for (int i = 0; i < n; i++) {
    printf("%d\n", myrand());
  }

  return 0;
}

(code/custom_lcg.c)

Custom LCG implementation (3/3)

By executing it we get

gcc custom_lcg.c -o custom_lcg

[leo@archlinux code]$ ./custom_lcg 
2147458185
483737
2138292585
174630137
976994632
764454763
507744979
1090263579
759828418
595645533

Now if we use attack_lcg.py to extract the parameters

outputs = [2147458185, 483737, 2138292585, 174630137,
           976994632, 764454763, 507744979, 1090263579,
           759828418, 595645533]

c = compute_modulus(outputs)
a = compute_multiplier(outputs, c)
b = compute_increment(outputs, c, a)

print(f"c={c}")    
print(f"a={a}")
print(f"b={b}")

We get

[leo@archlinux code]$ python3 attack_lcg.py 
c=1
a=0
b=0

Why did it fail?

Did we break the math somehow?

The mathematical model on which our attack is based assumes to be working with the standard LCG formula

\[\begin{cases} x_0 &= \text{seed} \\ x_n &= (x_{n-1} \cdot a + b) \mod c \\ \end{cases}\]

Is this the case when working with C?

Someone said… what, overflows?

In C every datatype has a fixed number of bytes.

When all bytes of a given datatype (uint32_t) are used, an overflow happens.

Overflows break our model

The correct model when dealing with overflows is the following one

\[\begin{cases} x_0 &= \text{seed} \; \land \; \texttt{0xFFFFFFFF} \\ x_n &= (((x_{n-1} \cdot a) \; \land \; \texttt{0xFFFFFFFF} + b) \\ &\;\;\;\;\;\;\;\;\;\;\; \land \; \texttt{0xFFFFFFFF} ) \mod c \\ \end{cases}\]

When things break down, asses your models.

(works in all aspects of life, btw)

So, now what?

We have mentioned that

Now we can see why this is the case.

Indeed, we have described two different PRNGs:

• Middle Square Method
• Linear Congruential Generator

And we learned how to bypass the "randomness" they produce in order to predict the next number.

So, now what do we do?

Are we doomed to use cryptographically unsafe generators of pseudo-randomness?

Luckily for us, no!

(sort of…)

Towards CSPRNG

And here comes a new term:

\[\begin{split} \text{CSPRNG} &\longrightarrow \text{Cryptographically} \\ &\longrightarrow \text{Secure} \\ &\longrightarrow \text{Pseudo} \\ &\longrightarrow \text{Random} \\ &\longrightarrow \text{Number} \\ &\longrightarrow \text{Generator} \\ \end{split}\]

A CSPRNG has to satisfy the following two properties:

• Next-bit test
• State compromise extensions

Next-bit test (1/2)

Given the first \(k\) bits of a random sequence, there is no polynomial-time algorithm that can predict the \((k+1)\) th bit with probability of success better than \(50\%\).

Next-bit test (2/2)

This is to say:

no matter how many outputs I see, I'm not gonna have a good time trying to predict the next generated value

\[x_0, x_1, x_2, \ldots, x_n \longrightarrow \text{?}\]

State compromise extensions (1/2)

In the event that part or all of its state has been revealed (or guessed correctly), it should be impossible to reconstruct the stream of random numbers prior to the revelation.

State compromise extensions (2/2)

Additionally, if there is an entropy input while running, it should be infeasible to use knowledge of the input's state to predict future conditions of the CSPRNG state.

CSPRNG vs PRNG (1/3)

CSPRNG vs PRNG (2/3)

CSPRNG vs PRNG (3/3)

import random
import secrets

def main():
    figure, axis = plt.subplots(1, 2)
    n = 1000000
    max_int = 100
    csprng_out = [0] * n
    for k in range(0, n):
        csprng_out[k] = secrets.randbelow(max_int)
    prng_out = [0] * n
    for k in range(0, n):
        prng_out[k] = random.randrange(0, max_int)
    axis[0].hist(csprng_out, max_int, rwidth=0.5, color="red")
    axis[0].set_title("CSPRNG")
    axis[1].hist(prng_out, max_int, rwidth=0.5, color="blue")
    axis[1].set_title("PRNG")
    plt.show()
    
if __name__ == "__main__":
    main()

(code/csprng_vs_prng.py)

Now…

there are various ways to access CSPRNGs.

CSPRGNs Implementations (1/4)

In linux you can use the device driver /dev/urandom

$ head -c 500 /dev/urandom > test.txt

$ ls -lha random_data
-rw-r--r-- 1 leo users 500  6 ott 15.58 random_data

$ hexdump -C random_data 
00000000  84 97 11 56 8f 67 4b 1f  d4 82 85 27 47 79 1a 8c  |...V.gK....'Gy..|
00000010  78 f1 14 1f 23 98 ea e1  84 96 ae be f7 d9 ac 9a  |x...#...........|
00000020  b3 be 3b 41 7a 93 fa 06  d9 86 5b fb bc da 26 3c  |..;Az.....[...&<|
                                                                        ...

CSPRGNs Implementations (2/4)

In python you can use the os.urandom() function

#!/usr/bin/env python3

import os

def generate_random_digest(bit_size):
    return os.urandom(bit_size).hex()

if __name__ == "__main__":
    print(generate_random_digest(8))
    print(generate_random_digest(16))
    print(generate_random_digest(32))

(code/csprng.py)

CSPRGNs Implementations (3/4)

$ python3 csprng.py 
8d7d442ef029b7c4
448903bb7f13a2a26414c4b73e0c0014
4e2bd3fb9b70aa38a626aa8262d9dd3acd843e79cdd08efe18221b7b17f833d9

CSPRGNs Implementations (4/4)

You can also use the secrets library

Q: are CSPRGNs always better?

Q: are CSPRGNs always better?

A: No, of course not.

They are more expensive, since entropy is hard to generate.

Therefore they should only be used for security reasons.

To Finish, A Big Picture

Big picture (1/4)

Through PRNGs we are able use pseudo-randomness for various purposes.

Big picture (2/4)

Remember however that pseudo-randomness is not true randomness.

Big picture (3/4)

Before using PRNGs, ask yourself:

Is it a problem if a human mind is able to guess the next number?

Big picture (4/4)

Q: Is it a problem if a human mind is able to guess the next number?

If it is, go with CSPRGNs, otherwise stick with classical PRNGs.

That's it.

Thank you.