Capture The Flags

A (somewhat) gentle introduction

Leonardo Tamiano

On Capture The Flags (CTFs)
The Black-Box Technique
- Example of Black Boxing
- Interfaces and Implementations
Python Review
Out First Challenges
- Caesar Cipher
- One-Time Pad
Your Turn
- Many-Times Pad
- LCG Lottery

On Capture The Flags (CTFs)

Capture The Flags are offline/online events that focus on computer security related topics.

The idea is to have a series of challenges, and the goal of each challenge is to capture a flag.

\[\text{Flag\{Crypt0IsH4rd\}}\]

The flag is protected by various mechanism, and to get it one has to find, research and exploit one or more vulnerabilities.

Each challenge belongs within a specific category.

binary
reverse
web
crypto
mobile
OSINT

Learning through CTFs can be fun and instructive.

\[\textbf{University} \Leftrightarrow \textbf{CTFs} \Leftrightarrow \textbf{Real-World}\]

The Black-Box Technique

Computer Science is complex.

Applied cryptography is very complex.

Q: How do you deal with such overwhelming complexity?

Helpful idea:

being able to think in terms of

black boxes

Q: What is a black box?

A: It is anything that takes an input and produces an output.

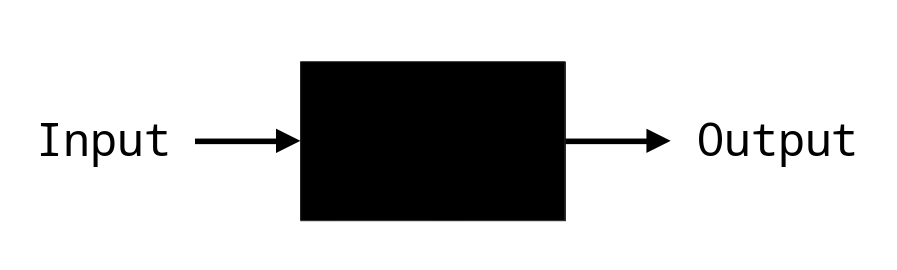
Thinking in terms of black boxes allows us to

ignore implementation details!

When using black boxes we're only interested in the mapping

\[\text{Input} \longrightarrow \text{Output}\]

This can remove a lot of complexity.

(but be careful cause you're gonna miss some details)

Example of Black Boxing

Example of Black Boxing (1/4)

Consider the following code

def fun(arr, n):
    gap = n // 2
    while gap > 0:
        for i in range(gap, n):
            temp = arr[i]
            j = i
            while (j >= gap and arr[j - gap] > temp):
                arr[j] = arr[j - gap]
                j -= gap
            arr[j] = temp
        gap //= 2

(code/black-box.py)

Example of Black Boxing (2/4)

We can analyze the previous code in various ways.

If we "black box it" we're only interested in the mapping between input and output.
If we "white box it" we're also interested about its implementation details.

Example of Black Boxing (2/4)

We can test the code as follows

def main():        
    arr = [3, 5, 2, 1, 0, 2, 3, 1]
    n = len(arr)
    print(arr)
    fun(arr, n)
    print(arr)

Example of Black Boxing (3/4)

Executing it, we get

$ python3 black-box.py 
Before function call
[3, 5, 2, 1, 0, 2, 3, 1]
After function call
[0, 1, 1, 2, 2, 3, 3, 5]

What does the code do?

It sorts an array of integers (shell-sort)!

Interfaces and Implementations

When analyzing real software implementations, it is impossible to understand all the details.

Thinking in terms of black boxes therefore becomes a necessity.

Of course, a black box is simply an abstraction.

A model to help us not go crazy.

A black box is simply an abstraction.

Thus, it is always important to be extremely aware of what exactly is that we are "black boxing" at any given moment.

I suggest to always keep a mental boundary between

Interface Knowledge (black box)
Implementation Knowledge (white box)

I also suggest to try to implement things yourself, so as to develop more implementation knowledge.

Implementation

(white box)

def fun(arr, n):
    gap = n // 2
    while gap > 0:
        for i in range(gap, n):
            temp = arr[i]
            j = i
            while (j >= gap and arr[j - gap] > temp):
                arr[j] = arr[j - gap]
                j -= gap
            arr[j] = temp
        gap //= 2

Interface

(black box)

\[\begin{split} \text{arr} = \{x_0, &x_1, x_2, \ldots, x_n\} \\ &\downarrow \\ \text{fun}(&\text{arr}, n) \\ &\downarrow \\ \text{arr} = \{x_{i_0}, &x_{i_1}, x_{i_2}, \ldots, x_{i_n}\} \\ i_j \leq i_k &\implies x_{i_j} \leq x_{i_k} \end{split}\]

Confuse interfaces with implementations and sooner or later you will be in much trouble (imho)

The dualism

\[\text{Interface Knowledge}\]

\[\updownarrow\]

\[\text{Implementation Knowledge}\]

applies to all sorts of technologies.

Even cars…

Implementation

(white box)

Interface

(black box)

I suspect it is an intrinsic property of technology.

Of the two, I believe implementation knowledge is much rarer, and, therefore, potentially more valuable.

Python Review

CTFs involve a diverse and heterogeneous set of technologies.

We will restrict your focus on python.

Q: What is Python?

Python is an interpreted programming language that can be used in many different contexts

Data science
Cybersecurity
Web development
DevOps

Q: Interpreted?

There exists a program, the interpreter, which takes in input python code and which executes each line of the code to produce an effect.

\[\text{Python code} \longrightarrow \text{Python Interpreter} \longrightarrow \text{Effect}\]

\[\text{010101010111010101110101010101}\]

We write code to change bits

\[\text{101010101000101010001010101010}\]

There are various online tutorials on how to install python in your environment.

https://www.python.org/downloads/

Basic structure of a python program

#!/usr/bin/env python

def main():
    print("Hello World!")

if __name__ == "__main__":
    main()

(code/python-review/hello.py)

NOTE: The code is executed from top to bottom.

$ python3 hello.py 
Hello World!

I suggest you to (briefly) review the following basic programming construct:

variables
functions
conditionals
iteration
basic data structures
classes

NOTE: No need to be an expert

Variables in Python

#!/usr/bin/env python

if __name__ == "__main__":
    boolean = True
    integer = 10
    floating = 10.5
    string = "Hello"

(code/python-review/variables.py)

Functions in Python

#!/usr/bin/env python

def my_sum(a, b):
    return a + b

if __name__ == "__main__":
    result = my_sum(3, 5)
    print(result)

(code/python-review/functions.py)

Conditionals in Python

#!/usr/bin/env python

def absolute_value(a):
    if a > 0:
        return a
    else:
        return -a

if __name__ == "__main__":
    print(absolute_value(-10))
    print(absolute_value(10))

(code/python-review/conditionals.py)

Iterations in Python

#!/usr/bin/env python

def check_prime(n):
    for i in range(0, n):
        if n % i == 0:
            return False
    return True

if __name__ == "__main__":
    print(check_prime(7))
    print(check_prime(10))

(code/python-review/iterations.py)

Basic data structures in Python

#!/usr/bin/env python

if __name__ == "__main__":
    my_list = [10, 13, 3, 0, 6]
    first_element = my_list[0]
    last_element = my_list[4]
    length = len(my_list)
    
    my_dictionary = {"a": 0, "b": 0, "c": 0}
    value = my_dictionary["a"]
    my_dictionary["d"] = 0

    my_tuple = (10, 20)
    elem = my_tuple[0]

(code/python-review/data-structures.py)

Classes in Python

#!/usr/bin/env python

class Person:
    def __init__(self, name, age):
        self.name = name
        self.age = age

    def set_age(self, age):
        self.age = age

    def get_age(self):
        return self.age

if __name__ == "__main__":
    p1 = Person("Leonardo", 27)
    p2 = Person("Giuseppe", 22)
    print(p1.get_age())

(code/python-review/classes.py)

Out First Challenges

Let's start by analyzing some challenges together.

Caesar Cipher

The idea of a Caesar Cipher is to hide the meaning of a message by shifting each letter of the alphabet by a specific constant \(c=3\).

Shift when \(c=3\)

For a single letter

\[\text{A} \longrightarrow \text{A} + 3 = \text{D}\]

Shift when \(c=3\)

For the entire alphabet

\[\begin{split} &\text{ABCDEFGHIJKLMNOPQRSTUVWXYZ} \\ &\qquad \qquad \qquad \qquad \downarrow \\ &\text{DEFGHIJKLMNOPQRSTUVWXYZABC} \\ \end{split}\]

Applying Caesar Cipher

\[\begin{split} &\text{HELLO WORLD} \\ &\;\;\;\;\;\;\;\;\;\;\;\downarrow \\ &\text{KHOOR ZRUOG} \end{split}\]

The Challenge (1/2)

We are given a file chal.txt with the following content

BHWC{ODEBPEJC_EO_JKP_AJKQCD!}

and we need to recover the flag

FLAG{...}

The Challenge (2/2)

We're also given the code that wasa used to generate chal.txt

def main():
    shift_value = random.randint(0, 25)
    c = Caesar(shift=shift_value)
    with open("chal.txt", "w") as f:
        encrypted_flag = c.encrypt(FLAG)
        f.write(encrypted_flag)

How would you solve it?

Hint: KNOWN-PLAINTEXT ATTACK

KNOWN-PLAINTEXT ATTACK

The plaintext flag starts with \(\text{F}\). We can use this fact to compute the shift used.

\[\text{shift} = \text{ASCII}(c_1) - \text{ASCII}(F) \mod 26\]

Where \(c_1\) is the first letter of the ciphertext

In our case

\[\begin{split} \text{shift} &= \text{ASCII}(c_1) - \text{ASCII}(F) \mod 26 \\ &= \text{ASCII}(B) - \text{ASCII}(F) \mod 26 \\ &= 66 - 70 \mod 26 \\ &= - 4 \mod 26 \\ &= 22 \end{split}\]

Implemented in code

#!/usr/bin/env python3

from caesar import Caesar

def solve():
    flag = open("./chal.txt", "r").read()
    
    # extract shift_value with a KNOWN PLAINTEXT ATTACK
    shift_value = (ord(flag[0]) - ord('F')) % 26

    # decipher the rest
    c = Caesar(shift=shift_value)
    decrypted_flag = c.decrypt(flag) 
    print(decrypted_flag)
    
if __name__ == "__main__":
    solve()

$ python3 solution.py 
FLAG{SHIFTING_IS_NOT_ENOUGH!}

One-Time Pad

This challenge starts with the following text

Who needs AES when you have XOR?

The challenge is made up of two files

A challenge.py python script

An output.txt file with the following content

Flag: 134af6e1297bc4a96f6a87fe046684e8047084ee046d84c5282dd7ef292dc9

(code/one-time-pad)

The python script contains the following code

#!/usr/bin/python3
import os
flag = open('flag.txt', 'r').read().strip().encode()

class XOR:
    def __init__(self):
        self.key = os.urandom(4)
    def encrypt(self, data):
        xored = b''
        for i in range(len(data)):
            xored += bytes([data[i] ^ self.key[i % len(self.key)]])
        return xored
    def decrypt(self, data):
        return self.encrypt(data)

def main():
    global flag
    crypto = XOR()
    print ('Flag:', crypto.encrypt(flag).hex())

if __name__ == '__main__':
    main()

(code/one-time-pad/challenge.py)

We can infer that the output.txt file was encrypted using the XOR class defined in challenge.py.

In particular, the code implements a one-time-pad.

The idea behind the one-time-pad is to compute the encrypted text by using the XOR operation between the original message bytes and a random key.

\[\text{Plaintext} \mathbin{\oplus} \text{Random key} \longrightarrow \text{Encrypted text}\]

To work properly, the scheme requires that:

The key must be generated using cryptographically secure pseudo-random bytes.
The key must be as long as the message.
For each message, a new key must be generated.

Is this the case?

class XOR:
    def __init__(self):
        self.key = os.urandom(4)
        
    def encrypt(self, data):
        xored = b''
        for i in range(len(data)):
            xored += bytes([data[i] ^ self.key[i % len(self.key)]])
        return xored
    
    def decrypt(self, data):
        return self.encrypt(data)

(code/one-time-pad/challenge.py)

The initialization of the key is done using os.urandom(), which provides with cryptography safe random bytes.

def __init__(self):
    self.key = os.urandom(4)

(code/one-time-pad/challenge.py)

Decryption is the same as encryption

def decrypt(self, data):
    return self.encrypt(data)

(code/one-time-pad/challenge.py)

Finally, encryption is done by xoring the byte of the message with the byte of the key

def encrypt(self, data):
    xored = b''
    for i in range(len(data)):
        xored += bytes([data[i] ^ self.key[i % len(self.key)]])
    return xored

(code/one-time-pad/challenge.py)

What happens when

        len(data) > len(self.key)

        len(data) > len(self.key)

At some point the bytes of the keys are re-used again, even though this shouldn't be possible.

This vulnerability breaks the implementation.

Indeed, we can extract all key bytes by doing, once again, a KNOWN-PLAINTEXT ATTACK

\[\begin{split} K_0 &= C_0 \mathbin{\oplus} \text{ASCII}(F) \\ K_1 &= C_1 \mathbin{\oplus} \text{ASCII}(L) \\ K_2 &= C_2 \mathbin{\oplus} \text{ASCII}(A) \\ K_3 &= C_3 \mathbin{\oplus} \text{ASCII}(G) \\ \end{split}\]

NOTE: This is enough to break the entire ciphertext.

Solution

#!/usr/bin/env python3

def solve():
    with open("./output.txt", "r") as f:
        output = f.read()
        flag = output.split("Flag: ")[1]
        encrypted_bytes = bytes.fromhex(flag)

        # extract key bytes
        key = [0, 0, 0, 0]
        key[0] = encrypted_bytes[0] ^ ord('F')
        key[1] = encrypted_bytes[1] ^ ord('L')
        key[2] = encrypted_bytes[2] ^ ord('A')
        key[3] = encrypted_bytes[3] ^ ord('G')

        # decrypt flag
        plaintext = ["A"] * len(encrypted_bytes)
        for i in range(0, len(encrypted_bytes)):
            plaintext[i] = chr(encrypted_bytes[i] ^ key[i % 4])
        plaintext = "".join(plaintext)

        print(plaintext)

(code/one-time-pad/solution.py)

Your Turn

Many-Times Pad

They told me to use it one time.
But really, what's the issue here if I use it more than once?

Many-Times pad

FILES: https://teaching.leonardotamiano.xyz/university/2023-2024/cns/02/many-times-pad.zip
IP: 204.216.217.175
PORT: 4321

We can explore the challenge with nc

$ nc 204.216.217.175 4321
Welcome to Many-times pad.

Make a choice:
 [1] Show flag
 [2] Encrypt

With option 1 we receive a base64 encoded falg

Flag: 75SMMJiMn3fLPCFP+ubDEAwL1cXgYF7s8XN4Stqg

If we decode it however we see unrecognizable bytes

$ echo "75SMMJiMn3fLPCFP+ubDEAwL1cXgYF7s8XN4Stqg" | base64 -d | hexdump -C

ef 94 8c 30 98 8c 9f 77  cb 3c 21 4f fa e6 c3 10  |...0...w.<!O....|
0c 0b d5 c5 e0 60 5e ec  f1 73 78 4a da a0        |.....`^..sxJ..  |

NOTE: This means the flag is encrypted!

With option 2 we can send an arbitrary input

Send data to encrypt:
HELLOWORLD

However that input has to be base64 encoded before, otherwise we get an error message

[ERROR]: Could not understand data: make sure to base64 your payload!

With proper base64 input instead we get a response back

Send data to encrypt:
SEVMTE9XT1JMRAo=
Encrypted: g9SGPimPgvOcRIk=

This seems to be the relative encrypted version of our payload.

We can now analyze the source code of the server, server.py

Python Client (1/5)

Finally, we develop the following client application to interact with the server in the file client.py

#!/usr/bin/env python3

import socket
from base64 import b64decode
from base64 import b64encode

REMOTE_IP = "204.216.217.175"
REMOTE_PORT = 4321