On Padding Oracles

0x01 – The Challenge

We will learn about CBC-PKCS#7 padding oracles through a challenge called

Yet Another Oracle

Yet Another Oracle

Challenge Overview (1/8)

The challenge is made up of a single python script, server.py, which implements a basic TCP server written in python.

Challenge Overview (2/8)

The challenge is started server-side

$ python3 server.py 
[INFO] - Start of challenge: Yet Another Oracle
[INFO] - Listening on 4444...

Challenge Overview (3/8)

As soon as we connect we see the following

$ nc localhost 4444
Hi, I've been told to show you this.
====================================

ENCRYPTED_FLAG WITH CBC-AES:
 /s0/br/6DThDlXDzViyNwrcX0XbJihAV2a5ikLfp6r5mpNCGKe9lYtlVzuIfTLtz

> 

Challenge Overview (4/8)

We can interact with the challenge by sending an arbitrary amount of bytes, and the server replies with either \(\texttt{NOPE}\) or \(\texttt{OK!}\).

$ nc localhost 4444
Hi, I've been told to show you this.
====================================

ENCRYPTED_FLAG WITH CBC-AES:
 /s0/br/6DThDlXDzViyNwrcX0XbJihAV2a5ikLfp6r5mpNCGKe9lYtlVzuIfTLtz

> test
NOPE
> /s0/br/6DThDlXDzViyNwrcX0XbJihAV2a5ikLfp6r5mpNCGKe9lYtlVzuIfTLtz
OK!

Challenge Overview (5/8)

In terms of code, we have the following

def challenge_3_main():
    global CHALLENGE_NAME, PORT, IV, KEY, CIPHER, ENCRYPTED_FLAG
    
    IV = get_random_bytes(AES.block_size)
    KEY = get_random_bytes(AES.block_size)
    CIPHER = AES.new(KEY, AES.MODE_CBC, IV)
    
    data_to_encrypt = b"A" * 16 + FLAG
    ENCRYPTED_FLAG = b64encode(CIPHER.encrypt(pad(data_to_encrypt, AES.block_size)))
    
    print(f"[INFO] - Start of challenge: {CHALLENGE_NAME}")
    print(f"[INFO] - Listening on {PORT}...")

    socketserver.TCPServer.allow_reuse_address = True
    server = ReusableTCPServer(("0.0.0.0", PORT), incoming)
    server.serve_forever()

Challenge Overview (6/8)

When a client connects to the server the challenge function is executed

def challenge(req):
    global IV, KEY, CIPHER, ENCRYPTED_FLAG
    req.sendall(b'Hi, I\'ve been told to show you this.\n' +\
                b'====================================\n\n' +\
                b'ENCRYPTED_FLAG WITH CBC-AES: ' +\
                ENCRYPTED_FLAG + b'\n\n> ')
    time.sleep(0.2)
    while True:
        try:
            client_payload = req.recv(4096)
            if len(client_payload) > 0:
                oracle_output = oracle(client_payload)
                if oracle_output == True:
                    req.sendall(b'OK!\n> ')
                else:
                    req.sendall(b'NOPE\n> ')
            
        except Exception as e:
            print(e)
            exit()

Challenge Overview (7/8)

The oracle function checks for PKCS#7 conformity

def oracle(payload):
    global IV, KEY, CIPHER    
    try:
        payload = b64decode(payload)
        CIPHER = AES.new(KEY, AES.MODE_CBC, IV)        
        decrypted_payload = CIPHER.decrypt(payload)
        unpadded_payload = unpad(decrypted_payload, AES.block_size)
        return True
    except ValueError as e:
        return False

Challenge Overview (8/8)

The objective of the challenge is to

0x02 – The Knowledge

The code of the challenge is vulnerable to a

CBC-PKCS#7 padding oracle attack

Q: What is a padding oracle attack?

Q: What is a padding oracle attack?

A: To understand This vulnerability we need to review the following concepts

• Block ciphers in CBC mode
• PKCS #7 padding
• MAC-then-ENCRYPT
• Cryptographic Oracles

Let's understand in detail each part.

AES-CBC

AES-CBC (1/7)

An example of block cipher is AES, which has a block size of \(128\) bits.

\[\underbrace{\texttt{01}\ldots\texttt{101}}_{\text{plaintext (} 128 \text{ bits)}} \longrightarrow \text{AES} \longrightarrow \underbrace{\texttt{11}\ldots\texttt{001}}_{\text{ciphertext (} 128 \text{ bits)}}\]

AES-CBC (2/7)

In CBC mode, each block of plaintext is XORed with the previous ciphertext block before being encrypted.

AES-CBC (3/7)

AES-CBC encryption formula

AES-CBC (4/7)

In terms of decryption we have

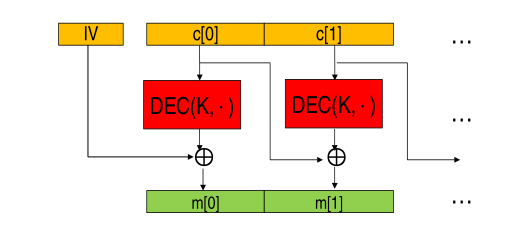
AES-CBC (5/7)

AES-CBC decryption formula

AES-CBC (6/7)

When using AES in CBC mode we introduce an Initialization Vector (IV), which must be carefully handled.

NOTE: Predictable IVs could lead to a different vulnerability, which is attacked through the famous BEAST attack!

AES-CBC (7/7)

Given that AES is a block cipher, it only works on blocks of \(128\) bits.

What happens if our plaintext does not evenly divide into \(128\)?

Basic idea: padding.

PKCS #7 Padding

PKCS #7 padding (1/3)

Described in RFC 5652, PKCS #7 works as follows:

The value of each added byte is the number of bytes that are added

PKCS #7 padding (2/3)

With block size = 8 byte = 64 bit

PKCS #7 padding (3/3)

With block size = 16 byte = 128 bit

MAC-Then-Encrypt

MAC-Then-Encrypt (1/7)

By default, TLS implements a MAC-Then-Encrypt scheme for securing the integrity and confidentiality of a session.

MAC-Then-Encrypt (2/7)

When TLS is used with a block cipher such as AES-CBC, it works as follows:

1. MAC is computed on:
   • Internal sequence number (replay attacks)
   • TLS header
   • TLS record data
2. Padding is added.
3. Block encryption.

MAC-Then-Encrypt (3/7)

The problem with this construction is that the MAC is computed before the padding is added, which means…

MAC-Then-Encrypt (4/7)

In turns, this means that

an attacker can change the padding a valid TLS message

meanwhile

the server will not be able to recognize that such change has taken place.

MAC-Then-Encrypt (5/7)

Q: Is this a security problem?

A: Yes.

MAC-Then-Encrypt (6/7)

More specifically, if the attacker is also able to obtain a PKCS #7 oracle on the server, then the attacker can perform a CBC padding oracle attack in order to

MAC-Then-Encrypt (7/7)

Technically, we don't steal the key from the server.

We just force the server to use it indirectly.

Cryptographic Oracles

Cryptography Oracles (1/6)

As stated by Alan Turing in 1938 in his PhD

Let us suppose we are supplied with some unspecified means of solving number-theoretic problems; a kind of oracle as it were. We shall not go any further into the nature of the oracle apart from saying it cannot be a machine.

Cryptography Oracles (2/6)

We can visualize an oracle as a black box that answers specific questions.

\[\text{Question} \longrightarrow \text{Oracle} \longrightarrow \text{Answer}\]

Different types of oracles might answer for different questions.

Cryptography Oracles (3/6)

For example,

Let \(g_{(e, N)}\) be a function that takes in input a ciphertext \(c\) encrypted with the key \((e, N)\) and outputs \(0\) if the relative plainext \(m\) is even, or \(1\) if its odd.

Where

\[c = m^e \mod N\]

Cryptography Oracles (4/6)

The code of our challenge offers a PKCS#7 oracle:

• If the message we send, once decrypted, respects the rules of the PKCS#7 padding, we get \(\texttt{OK!}\)
• Otherwise, we get \(\texttt{NOPE}\).

Cryptography Oracles (4/6)

Let \(C\) be the ciphertext of the plaintext \(P\). We can formalize the oracle of the challenge as follows

Cryptography Oracles (5/6)

Code that implements the PKCS#7 oracle

    while True:
        try:
            client_payload = req.recv(4096)
            if len(client_payload) > 0:
                oracle_output = oracle(client_payload)
                if oracle_output == True:
                    req.sendall(b'OK!\n> ')
                else:
                    req.sendall(b'NOPE\n> ')            
        except Exception as e:
            print(e)
            exit()

Cryptography Oracles (6/6)

Code that implements the PKCS#7 oracle

def oracle(payload):    
    try:
        payload = b64decode(payload)
        CIPHER = AES.new(KEY, AES.MODE_CBC, IV)        
        decrypted_payload = CIPHER.decrypt(payload)
        unpadded_payload = unpad(decrypted_payload, AES.block_size)
        return True
    except ValueError as e:
        return False

We are now ready to describe the attack.

Remember all the requirements

• Server using block cipher, CBC mode, PKCS#7 padding
• Attacker able to change the padding of the message.
• Server exposes a PKCS#7 padding oracle.

0x03 – The Attack

Before describing the attack lets introduce some useful notation.

Useful notation (1/3)

• \(P_1, P_2, \ldots, P_m\), to denote plaintext blocks.
• \(C_1, C_2, \ldots, C_m\)., to denote ciphertext blocks.

Where \(m\) represents the total number of blocks.

Useful notation (2/3)

We use \(P_i^j\) and \(C_i^j\) to denote specific bytes within the various blocks as follows

\[\begin{split} P^{j}_i &:= j \text{-th byte of the } i \text{-th plaintext block} \\ C^{j}_i &:= j \text{-th byte of the } i \text{-th ciphertext block} \\ \end{split}\]

Useful notation (2/3)

Let \(n\) denote the byte length of the block cipher in use.

\[\begin{split} P_1 &:= P_1^1 \;,\; P_1^2 \;,\; &\ldots \;,\; P_1^n \\ &\;\downarrow \\ C_1 &:= C_1^1 \;,\; C_1^2 \;,\; &\ldots \;,\; C_1^n \\ \end{split}\]

For AES-128 we have \(n=16\).

Let \(C_1, C_2, C_3, \ldots\) be the various ciphertext blocks, and let \(\text{IV}\) be the initialization vector used to bootstrap the AES-CBC construction.

Remember the core AES-CBC equations…

We will now describe how an attacker is able to decrypt the second ciphertext block \(C_2\).

• What we have: \(\text{IV} \;\;,\;\; C_1 \;\;,\;\; C_2\)
• What we need: \(P_2\)

Consider only the first two blocks and the IV

\[C := \text{IV} \;\;,\;\; C_1 \;\;,\;\; C_2\]

We will find the last byte of \(P_2\) using the oracle exposed by the server in a process of trial and error.

• Is the last byte of \(P_2\) equal to \(\texttt{0x00}\)?
• Is the last byte of \(P_2\) equal to \(\texttt{0x01}\)?
• …
• Is the last byte of \(P_2\) equal to \(\texttt{0xFF}\)?

Consider then the following question

Q: Is the last byte of \(P_2\) equal to \(\texttt{0x41}\)?

(\(\texttt{0x41} = \texttt{A}\), using ascii encoding)

Using our notation, we can write

\[P_2^n = \texttt{0x41} \;\texttt{?}\]

\(P_2^n = \texttt{0x41} \;\texttt{?}\)

Idea: start from \(C_1\) and construct\(\hat{C}_1\)

NOTE: Careful on those magic values \(\texttt{0x41} \;, \texttt{0x01}\).

We then use \(\hat{C}_1\) to construct a new ciphertext

\[\begin{split} C &= \text{IV} \;,\; C_1 \;,\; C_2 \;\;\;\; \text{(old ciphertext)} \\ &\downarrow \\ \hat{C} &= \text{IV} \;,\; \hat{C}_1 \;,\; C_2 \;\;\;\; \text{(new ciphertext)} \\ \end{split}\]

We then send the new ciphertext \(\hat{C}\) to the oracle exposed by the server.

Two cases to analyze, depending on the oracle answer:

• \(O(\hat{C}) = 1\)
• \(O(\hat{C}) = 0\)

Case I: \(O(\hat{C}) = 1\)

Suppose that the plaintext \(\hat{P}\) associated with the ciphertext \(\hat{C}\) is correctly padded according to PKCS#7.

What can we infer?

Case I: \(O(\hat{C}) = 1\)

By definition, during AES decryption the last byte of \(\hat{P}\) is obtained by XORing together the last byte of \(\hat{C}_1\), which is the byte modified by the attacker, and the last byte obtained by applying the decryption procedure to \(C_2\).

Case I: \(O(\hat{C}) = 1\)

Case I: \(O(\hat{C}) = 1\)

In formula,

Case I: \(O(\hat{C}) = 1\)

For \(\hat{P}\) to be correctly padded we can have different scenarios

(only the first one is highly likely, as it makes less assumptions about the plaintext)

Case I: \(O(\hat{C}) = 0\)

What about the other case?

Well in this case we know for sure that

\[P_2^n \neq \texttt{0x41}\]

Therefore

\[\begin{split} O(\hat{C}) = 1 \;\; &\implies \;\; P_2^n = \texttt{0x41} \;\;,\;\; \text{highly likely} \\ \\ O(\hat{C}) = 0 \;\; &\implies \;\; P_2^n \neq \texttt{0x41} \;\;,\;\; \text{for sure} \\ \end{split}\]

If we have not yet discovered the value of \(P_2^n\) with our initial guess, we can proceed with the next guess for the same byte.

For example, having tried the byte \(\texttt{0x41}\), we can now try the next byte \(\texttt{0x42}\).

In general this means that with \(256\) questions we will discover the value of \(P_2^n\).

\[\begin{split} P_2^{n} &= \texttt{0x00} \; \texttt{?} \\ P_2^{n} &= \texttt{0x01} \; \texttt{?} \\ &\vdots \\ P_2^{n} &= \texttt{0xFF} \; \texttt{?} \\ \end{split}\]

If we have discovered the value of \(P_2^n\) we can proceed to discover the value for the next byte, \(P_2^{n-1}\).

\[P_2^{n-1} = \texttt{0x41} \; \texttt{?}\]

\(P_2^{n-1} = \texttt{0x41} \;\texttt{?}\)

Construction similar to the one showed before.

From \(C_1\) we construct\(\hat{C}_1\)

Where \(P_2^n\) is the value we discovered previously

We then use \(\hat{C}_1\) to construct a new ciphertext

\[\begin{split} C &= \text{IV} \;,\; C_1 \;,\; C_2 \;\;\;\; \text{(old ciphertext)} \\ &\downarrow \\ \hat{C} &= \text{IV} \;,\; \hat{C}_1 \;,\; C_2 \;\;\;\; \text{(new ciphertext)} \\ \end{split}\]

Suppose now the attacker sends this new ciphertext \(\hat{C}\) to the oracle, and the oracle replies with

\[O(\hat{C}) = 1\]

What can we infer?

By definition, it means that the relative plaintext \(\hat{P}\) is correctly padded according to PKCS#7.

There is only one possible scenario in which \(\hat{P}\) is correctly padded. And that is when

\[\hat{P}_2^{n-1} = \texttt{0x02}\]

By construction we have

We thus get

Therefore,

\[\begin{split} O(\hat{C}) = 1 \;\; &\implies \;\; P_2^{n-1} = \texttt{0x41} \;\; \\ \\ O(\hat{C}) = 0 \;\; &\implies \;\; P_2^{n-1} \neq \texttt{0x41} \;\; \end{split}\]

If we have not yet discovered the value of \(P_2^{n-1}\) we can proceed with the next guess for the same byte.

\[P_2^{n-1} = \texttt{0x42} \;\texttt{?}\]

If we have discovered the value of \(P_2^{n-1}\) we can proceed to discover the next byte

\[P_2^{n-2} = \texttt{0x42} \;\texttt{?}\]

\(P_2^{n-2} = \texttt{0x41} \;\texttt{?}\)

Q: \(P_2^{n-2} = \texttt{0x41}\)?

Where \(P_2^{n-1}\) and \(P_2^n\) were discovered previously.

And it continues like that, until we're able to decrypt the entire block

\[C_2 \longrightarrow P_2\]

Considerations

In order to decrypt \(C_1\) we would need to have access to the initialization vector (IV), which sometimes we do not.

The attack works pretty much the same for all blocks expect the last block. This is bacause the last block is the only block that is properly padded. This can introduce false positives.

For example, say that \(m=2\) and that

\[P^m_n = \texttt{0x10}\]

Then, we cannot use the previous construction

and \(C_1\) is properly padded, giving us a false positive.

0x04 – The Code

We are now ready to see the code that implements the attack just described.

decrypt_block (1/3)

def decrypt_block(encrypted_text, n, block_size=8):
    """ Decrypts the n-th block of the encrypted_text """
    assert n > 1, "Cannot decrypt first block as we don't know the IV"

    # are we the last block? this matter because the last block is the
    # only block that is properly padded, and therefore could cause a
    # false positive answer when guessing the last byte with the value
    # of 0x1. Since then the xor would eliminate, the ciphertext
    # woulnd't change and therefore we would simply submit the block
    # as it is.
    last_block = True if int(len(encrypted_text) / block_size) == n else False
    
    saved_bytes = bytes(encrypted_text[block_size * (n-2): block_size * (n-1)])
    guess_so_far = [0] * block_size    

decrypt_block (2/3)

    for i in range(0, block_size):
        msg = list(encrypted_text[:block_size * n])
        found = False
        for c in range(0, 256):
            if last_block and i == 0 and c == 1:
                # skip this to avoid false positives,
                continue
            padding = i + 1
            guess_so_far[block_size - 1 - i] = c            
            # prepare new msg depending on how far we've come within this single block
            for j in range(0, i + 1):
                global_index = block_size * (n - 1) - j - 1
                relative_index = block_size - j - 1
                msg[global_index] = saved_bytes[relative_index] ^ guess_so_far[relative_index] ^ padding

decrypt_block (3/3)

            # test new msg
            r = query_oracle(bytes(msg))
            if r:
                found = True
                if chr(c) in string.printable:
                    print(f"[{n}]: byte {block_size - i} is: {c}, {chr(c)}")
                else:
                    print(f"[{n}]: byte {block_size - i} is: {c}, non-printable byte")
                break

        if not found and last_block and i == 0:
            # since we have not found any other alternatives, we can
            # safely assume that this is the correct value
            guess_so_far[block_size - 1 - i] = 1

    return guess_so_far

Finally, the query_oracle is used to obtain the oracle from the server

def query_oracle(payload):
    global SOCK
    encoded_payload = b64encode(payload)
    SOCK.send(encoded_payload)
    oracle_reply = SOCK.recv(4096)
    return b"OK" in oracle_reply

Example Execution (1/3)

$ python3 solution.py 
[2]: byte 16 is: 84, T
[2]: byte 15 is: 80, P
[2]: byte 14 is: 49, 1
[2]: byte 13 is: 82, R
[2]: byte 12 is: 67, C
[2]: byte 11 is: 78, N
[2]: byte 10 is: 51, 3
[2]: byte 9 is: 45, -
[2]: byte 8 is: 78, N
[2]: byte 7 is: 51, 3
[2]: byte 6 is: 72, H
[2]: byte 5 is: 84, T
[2]: byte 4 is: 45, -
[2]: byte 3 is: 67, C
[2]: byte 2 is: 52, 4
[2]: byte 1 is: 77, M

Example Execution (2/3)

[3]: byte 16 is: 3, non-printable byte
[3]: byte 15 is: 3, non-printable byte
[3]: byte 14 is: 3, non-printable byte
[3]: byte 13 is: 83, S
[3]: byte 12 is: 85, U
[3]: byte 11 is: 48, 0
[3]: byte 10 is: 82, R
[3]: byte 9  is: 51, 3
[3]: byte 8  is: 71, G
[3]: byte 7  is: 78, N
[3]: byte 6  is: 52, 4
[3]: byte 5  is: 68, D
[3]: byte 4  is: 45, -
[3]: byte 3  is: 83, S
[3]: byte 2  is: 49, 1
[3]: byte 1  is: 45, -

Example Execution (3/3)

Plaintext obtained is: M4C-TH3N-3NCR1PT-1S-D4NG3R0US  

0x05 – Your Turn!

New CTF released on

ctf.leonardotamiano.xyz

It is called

Don't Touch My Cookie